|
Size: 18437
Comment: added Banchoff-Pohl "area"
|
Size: 18441
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 6: | Line 6: |
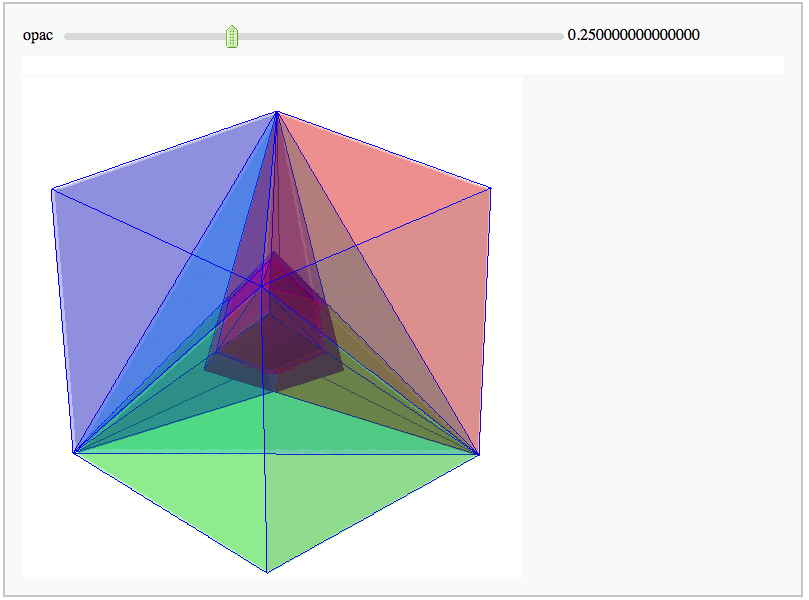
| == Intersecting tetrahedral reflections == | == Intersecting tetrahedral reflections FIXME == |
| Line 8: | Line 8: |
| {{{ | {{{#!sagecell |
| Line 12: | Line 12: |
| p12 = p1.union(p2) | p12 = p1.convex_hull(p2) |
| Line 15: | Line 15: |
| p34 = p3.union(p4) | p34 = p3.convex_hull(p4) |
| Line 18: | Line 18: |
| p56 = p5.union(p6) | p56 = p5.convex_hull(p6) |
| Line 21: | Line 21: |
| p78 = p7.union(p8) | p78 = p7.convex_hull(p8) |
| Line 36: | Line 36: |
| {{{ | {{{#!sagecell |
| Line 52: | Line 52: |
| normal=(gammap[1]/norma(gammap), -gammap[0]/norma(gammap)) | np=norma(gammap) |
| Line 54: | Line 54: |
| np=norma(gammap) | |
| Line 57: | Line 55: |
| pe=gammap[0]*gammapp[0]+gammap[1]*gammapp[1] | normal=(gammap[1]/np, -gammap[0]/np) |
| Line 80: | Line 79: |
| show(grafica,aspect_ratio=1,xmin=-2,xmax=2,ymin=-2,ymax=2)}}} | show(grafica,aspect_ratio=1,xmin=-2,xmax=2,ymin=-2,ymax=2) }}} |
| Line 86: | Line 86: |
| {{{ | {{{#!sagecell |
| Line 143: | Line 143: |
| }}} {{attachment:geodesics1.png}} {{{ |
# second interact |
| Line 197: | Line 195: |
| {{attachment:geodesics1.png}} | |
| Line 203: | Line 202: |
| {{{ | {{{#!sagecell |
| Line 247: | Line 246: |
| {{{ | {{{#!sagecell |
| Line 334: | Line 333: |
| }}} {{{ |
|
| Line 358: | Line 355: |
| print 'Aprox lenght using Crofton\'s formula: %f'%((cortes_tot/L)*(pi*M)) | print 'Approx length using Crofton\'s formula: %f'%((cortes_tot/L)*(pi*M)) |
| Line 366: | Line 363: |
| {{{ | {{{#!sagecell |
Sage Interactions - Geometry
goto interact main page
Contents
Intersecting tetrahedral reflections FIXME
by Marshall Hampton. Inspired by a question from Hans Schepker of Glass Geometry.
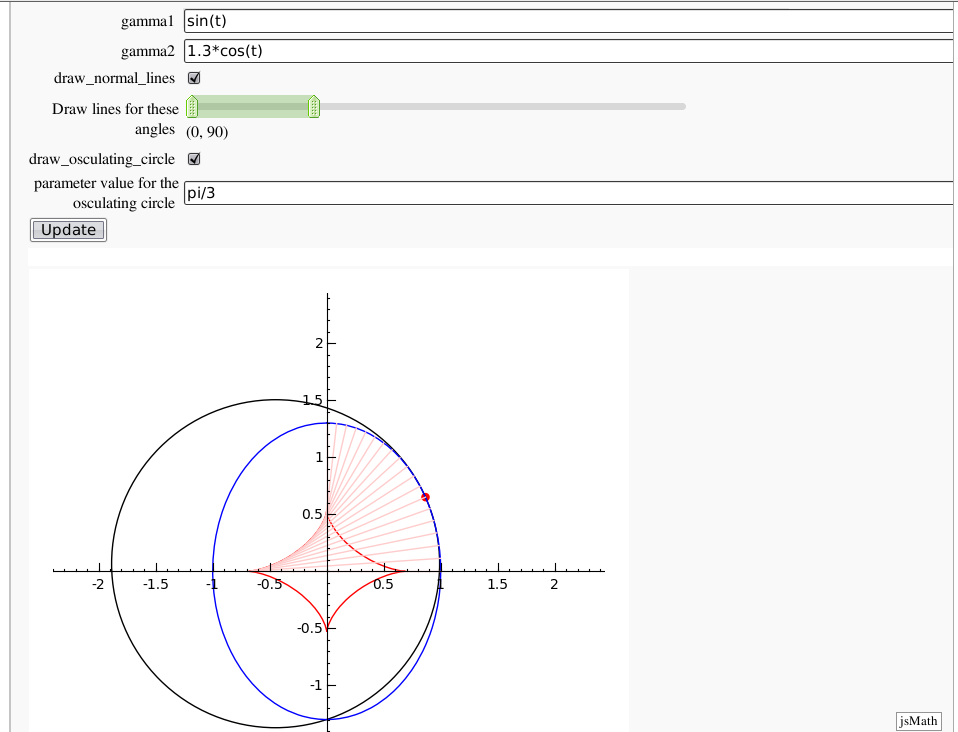
Evolutes
by Pablo Angulo. Computes the evolute of a plane curve given in parametric coordinates. The curve must be parametrized from the interval [0,2pi].
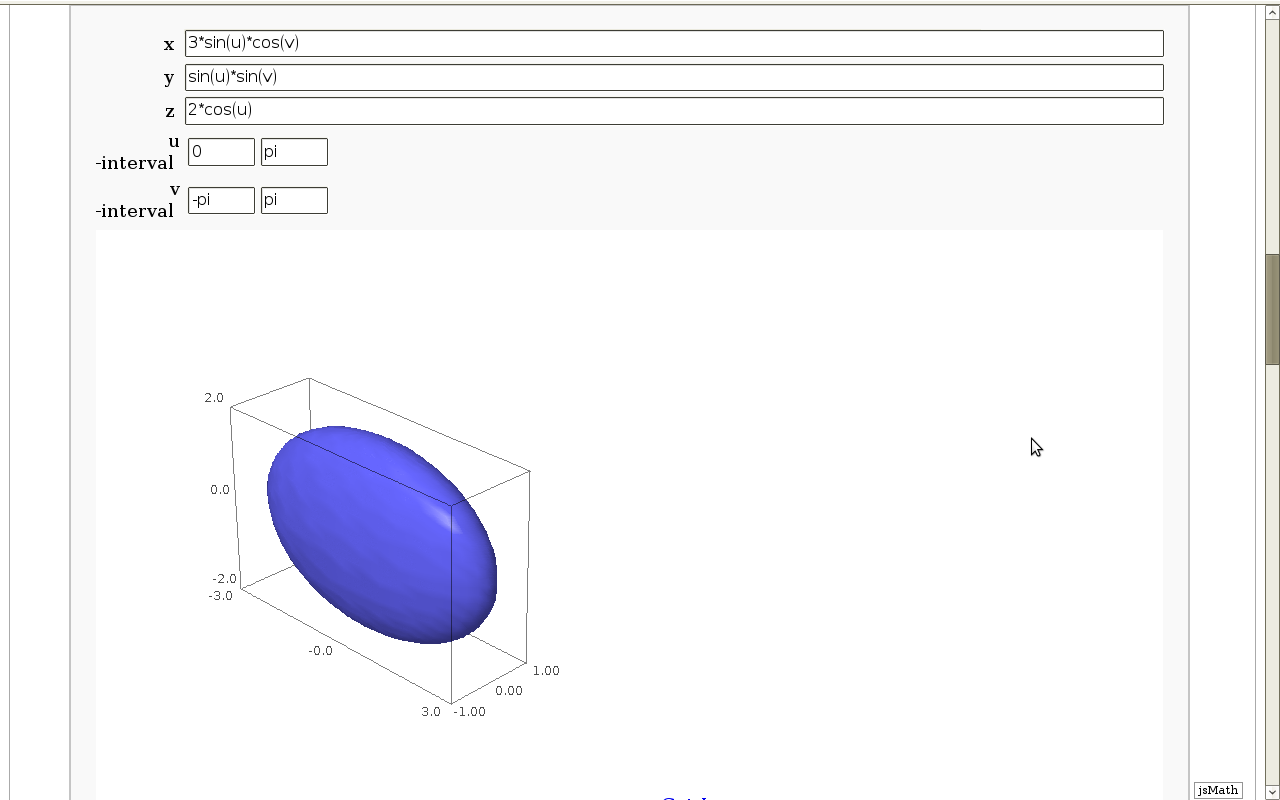
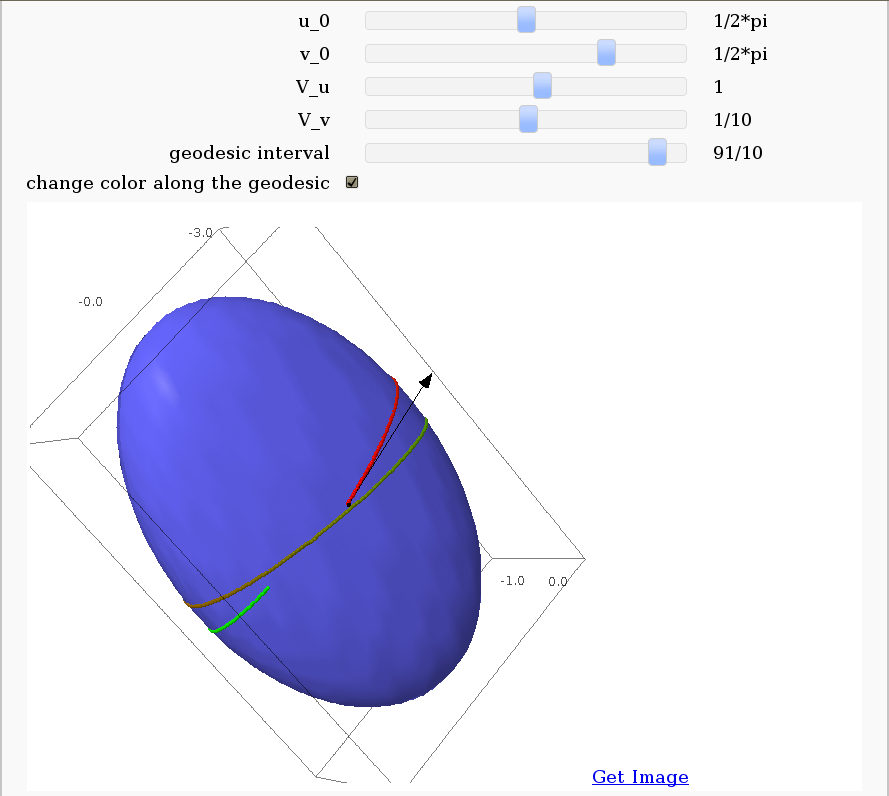
Geodesics on a parametric surface
by Antonio Valdés and Pablo Angulo. A first interact allows the user to introduce a parametric surface, and draws it. Then a second interact draws a geodesic within the surface. The separation is so that after the first interact, the geodesic equations are "compiled", and then the second interact is faster.
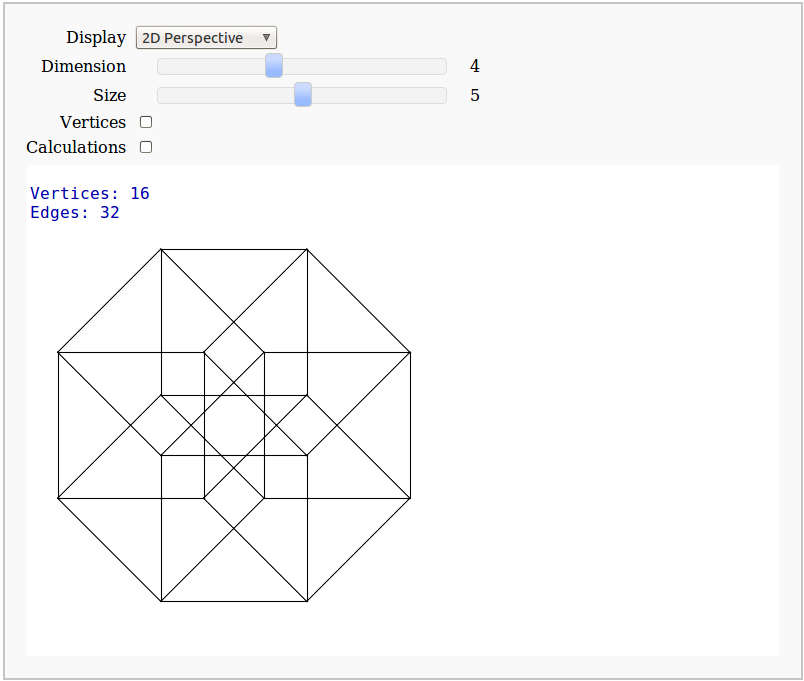
Dimensional Explorer
By Eviatar Bach
Renders 2D images (perspective or spring-layout) and 3D models of 0-10 dimensional hypercubes. It also displays number of edges and vertices.
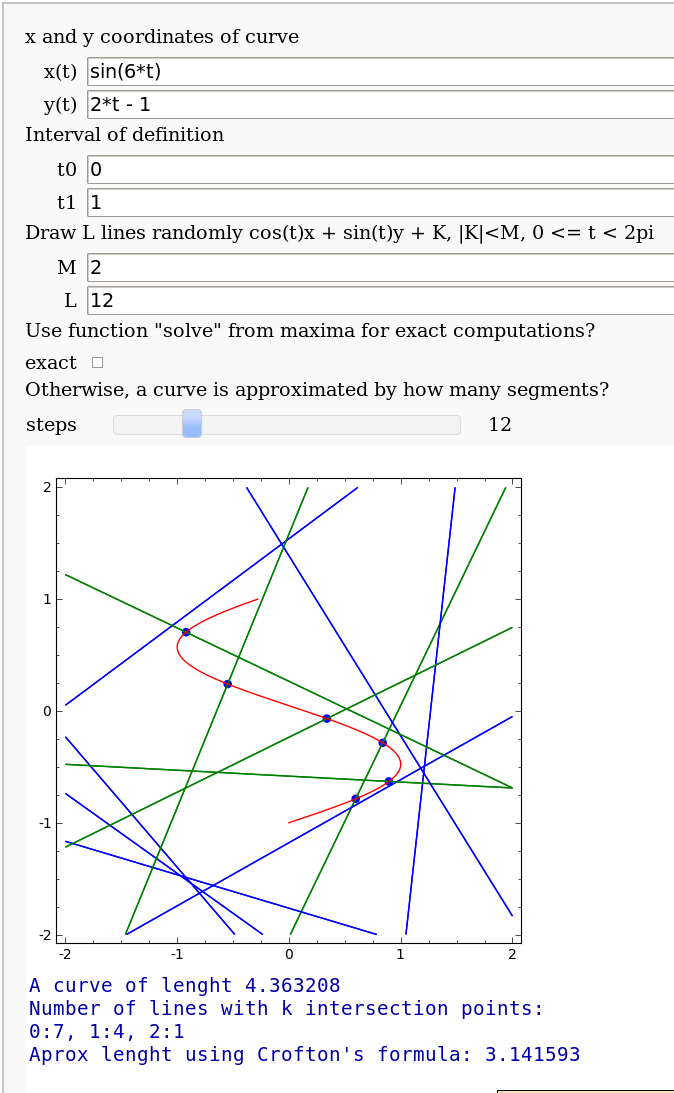
Crofton's formula
by Pablo Angulo. Illustrates Crofton's formula by throwing some random lines and computing the intersection number with a given curve. May use either solve for exact computation of the intersections, or may also approximate the curve by straight segments (this is the default).
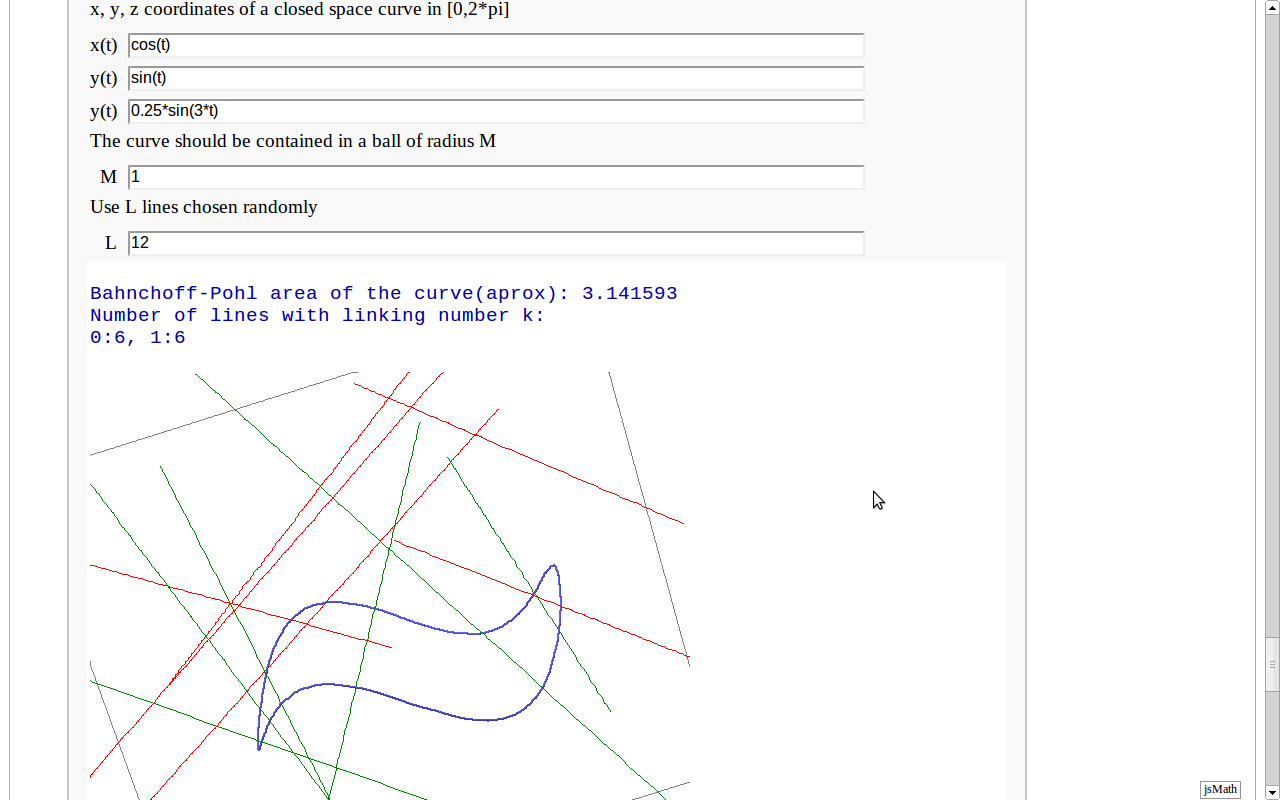
Banchoff-Pohl area
by Pablo Angulo. Computes the Banchoff-Pohl "area enclosed by a spatial curve", by throwing some random lines and computing the linking number with the given curve. Lines not linked to the given curve are displayed in red, linked lines are displayed in green.